[Pre-MBA 과정]

기초수학 세션

~~이게 어떻게 기초야?~~

약 9시간 강의내용 통합 정리하기

[기초수학 - 선형대수학과 미적분]

제1부: 선형대수학 (Linear Algebra)

선형대수학은 수많은 변수를 가진 방정식을 효율적으로 풀고, 이를 '공간'이라는 개념으로 시각화하여 데이터의 구조를 파악하는 학문이다.

1. 연립방정식과 해의 존재 (Systems of Equations)

우리가 구하고자 하는 미지수(x1,x2,x3) 가 여러 개일 때, 이를 풀기 위해서는 최소한 미지수의 개수만큼의 독립적인 식(행)이 필요하다.

Unique Solution: 미지수가 3개고 식도 3개일 때, 각 미지수가 딱 하나의 값으로 떨어지는 경우다.
무수히 많은 해: 만약 식의 개수가 부족하면(예: 미지수 3개, 식 2개), 정답은 하나로 정해지지 않는다. 이때는 x2=x3−2와 같이 한 문자를 다른 문자의 관계로 표현하게 된다. 이를 '자유 변수(Free Variable)'가 존재한다고 한다.

2. 벡터(Vector)와 스팬(Span)

데이터를 한 줄로 세운 것을 벡터라고 한다. 행렬의 각 열(Column)은 하나의 벡터로 취급할 수 있다.

벡터 표현: 방정식의 계수들을 따로 떼어 v1,v2,v3와 같은 벡터 형태로 만든다.
스팬(Span): 주어진 벡터들을 조합해서(더하거나 숫자를 곱해서) 만들 수 있는 모든 영역을 '스팬'이라 한다.
- 만약 어떤 결과값 가 이 영역 안에 없다면, "그 b는 v1,v2,v3의 스팬이 아니다"라고 말한다. 즉, 아무리 조합해도 그 값을 만들 수 없다는 뜻이다.
REF/RREF (Row Echelon Form): 복잡한 행렬을 가우스 소거법을 통해 계단 모양으로 단순화하는 과정이다. 이를 통해 해가 있는지, 스팬에 포함되는지를 판별한다. 만약 계산 과정에서 0=같은 모순이 나오면 해가 없는 것이다.

3. 선형 독립과 종속 (Linear Independence & Dependence)

데이터의 '중복성'을 판단하는 아주 중요한 개념이다.

선형 독립(Independent): 각 벡터가 독자적인 방향을 가지고 있어서, 다른 벡터들의 합이나 곱으로 표현될 수 없는 상태다. 데이터로 치면 "버릴 정보가 하나도 없는 상태"다.
선형 종속(Dependent): 어떤 벡터가 다른 벡터들의 조합(예:v2=v1+v3)으로 표현될 수 있는 상태다. 이는 정보의 중복을 의미하며, 차원을 낭비하고 있는 셈이다.

4. 행렬의 연산 (Matrix Operations)

행렬은 데이터의 묶음이며, 이를 곱하거나 뒤집는 연산에는 규칙이 있다.

행렬의 곱셈: 앞 행렬의 열(Column) 수와 뒤 행렬의 행(Row) 수가 같아야만 곱셈이 성립한다. 결과 행렬의 크기는 (앞 행렬의 행 수) × (뒤 행렬의 열 수)가 된다.
전치 행렬(Transpose,A^T ): 행과 열을 서로 맞바꾸는 것이다. 1행 2열에 있던 숫자가 2행 1열로 가는 식이다. 데이터 분석에서 행(관측치)과 열(변수)의 위치를 바꿔야 할 때 자주 쓰인다.

5. 역행렬(Inverse)과 행렬식(Determinant)

숫자에서 2의 역수가 1/2이듯, 행렬에도 원래 행렬과 곱해서 단위 행렬(1에 해당)이 되게 하는 '역행렬'이 존재한다.

행렬식(Determinant,ad−bc): 2x2 행렬에서 ad−bc로 계산되는 이 값은 행렬이 '역행렬을 가질 수 있는지'를 알려주는 판별식이다.
역행렬의 조건: 행렬식(ad−bc)이 0이 아니어야만 역행렬이 존재한다. 만약 이 값이 0이라면, 그 행렬은 정보를 잃어버린 상태이며 역연산이 불가능하다.

6. 가역 행렬 정리 (Invertible Matrix Theorem)

수업에서 언급된 "결국 다 같은 뜻이다"라는 부분이 바로 이 내용이다. 어떤 행렬 A에 대해 다음 문장들은 모두 동치(Equivalent)다. 하나가 참이면 나머지도 모두 참이다.

A의 역행렬이 존재한다.
A를 RREF로 만들면 단위 행렬(I)이 된다.
A의 열 벡터들은 서로 선형 독립이다.
Ax = b 는 오직 하나의 해(Unique Solution)를 갖는다.
A의 열 벡터들이 공간 전체를 스팬(Span)한다.

제2부: 미적분학 (Calculus) - 최적화

미적분은 데이터가 변하는 속도를 측정하고, 함수가 어디서 최대/최소를 갖는지(최적화)를 찾기 위한 도구다.

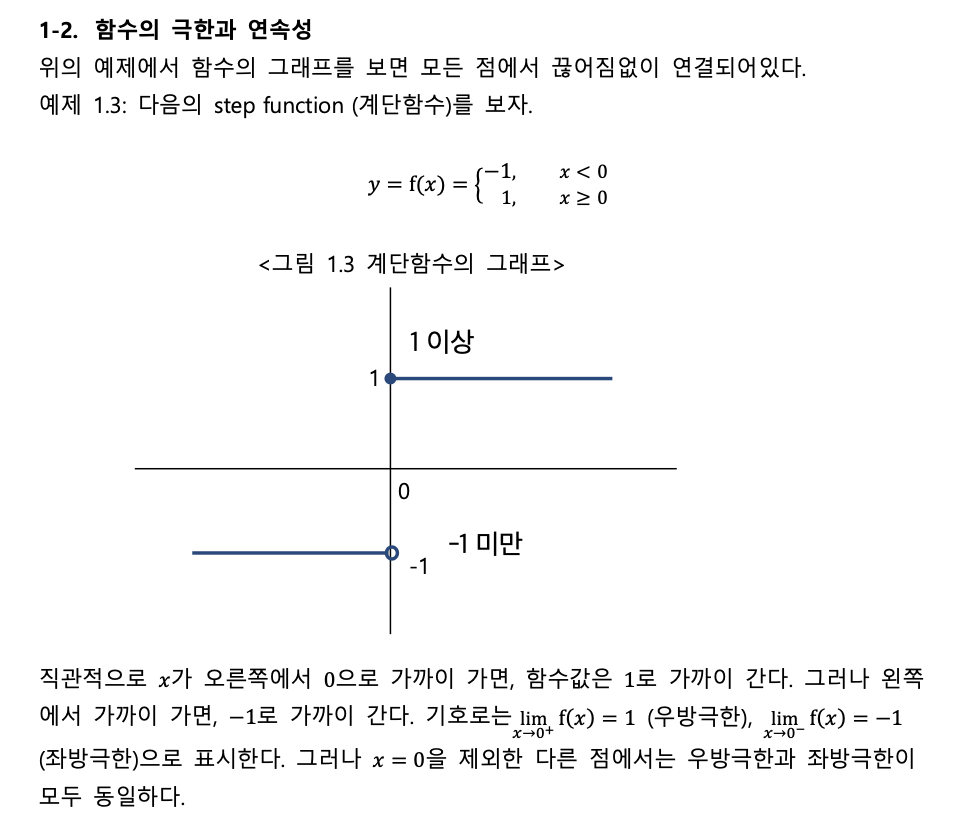
1. 극한(Limit)과 연속(Continuity)

미분을 정의하기 위한 밑바탕이다.

극한: 어떤 값에 무한히 가까이 다가갈 때의 목표값을 의미한다.
연속: 그래프가 끊기지 않고 이어진 상태다. 왼쪽에서 올 때의 값(좌극한)과 오른쪽에서 올 때의 값(우극한), 그리고 실제 그 점의 함숫값이 모두 같아야 '연속'이라고 한다.

2. 미분(Derivative) - 순간 변화율

원리: 어떤 점 에서 아주 미세한 변화(Δx)가 있을 때, y값이 얼마나 변하는지 그 기울기를 구하는 것이다.
목적: Δx를 0으로 보내어 '찰나의 순간'에 일어나는 기울기를 구한다. 이것이 바로 접선의 기울기다.
최적화(Optimization): 가장 많이 쓰이는 개념이다. 함수의 기울기가 0이 되는 지점을 찾으면, 그곳이 바로 이익이 최대가 되거나 비용이 최소가 되는 지점(극대/극소)일 확률이 높기 때문이다.
[중요] 미분계수와 도함수 (하단 사진)

3. 주요 미분 법칙 - 합성함수/다변수 함수

합성함수의 미분(Chain Rule): 함수 안에 함수가 들어있을 때(f(g(x))), 겉의 함수를 미분한 것에 안의 함수를 미분한 것을 곱하는 방식이다. 인공지능의 딥러닝(오차역전파)에서도 핵심 원리로 쓰인다.
다변수 함수의 미분(Partial Derivative): 변수가 여러 개(x,y,z…)일 때, 나머지 변수는 상수로 취급하고 특정 변수 하나에 대해서만 미분하는 것이다. 현실 데이터는 대부분 변수가 여러 개이므로 필수적인 개념이다.

3-2. 주요 미분 법칙 - 테일러 전개/매클로린 급수

테일러 급수(Taylor Series): 복잡한 함수를 다루기 쉬운 다항식(1차, 2차 함수 등)으로 근사(Approximation)하는 방법이다. 실제 복잡한 경제 모델을 단순화할 때 사용한다.

매클로린 급수(Maclaurin Series)
테일러 급수는 어떤 점 a를 기준으로 함수를 근사하는 방식이다. 여기서 기준점 a를 0으로 설정한 것이 바로 매클로린 급수이다. 즉, "0 근처에서 이 함수가 어떻게 움직이는지 다항식으로 표현해 보자"라는 아이디어에서 출발한다.

4. 적분(Integration) - 누적과 면적

적분은 미분의 반대 과정이다.

원리: 미분된 함수를 다시 원래대로 되돌리는 과정(부정적분)이며, 이때 사라졌던 상수항(C)을 붙여준다.
기하학적 해석: 그래프 아래의 면적을 구하는 것이다. 확률 밀도 함수에서 특정 구간의 확률을 구할 때(면적 구하기) 적분이 사용된다.
- 연결된 그래프 하단 면적을 그대로 구할 수는 없기 때문에, 직사각형으로 대신 해당 영역을 채워서 구한다.

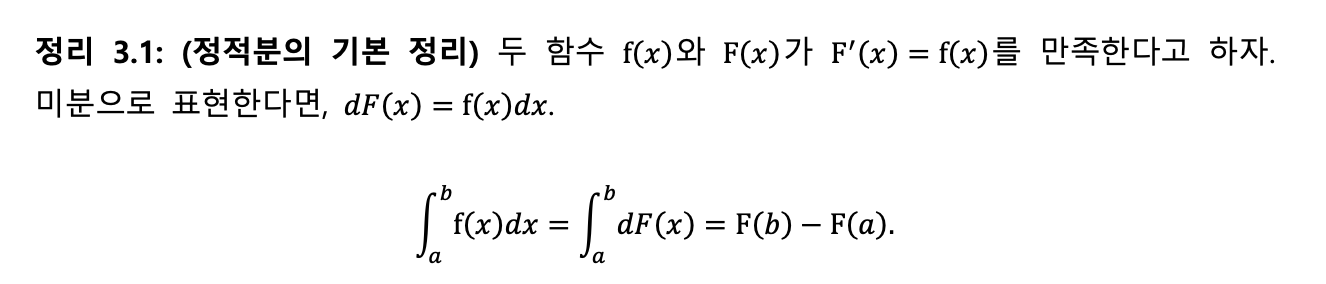
5. 최적화 이론(Optimization)

1. 극대·극소와 최대·최소 (Local vs Global)

함수의 그래프를 산맥이라고 상상해 보자. 최적화는 이 산맥에서 가장 낮은 골짜기나 가장 높은 봉우리를 찾는 과정이다.

극대값/극소값 (Local Maximum/Minimum): 내 주변 범위 내에서 내가 가장 높거나 낮은 지점이다. 동네 뒷산 봉우리 같은 개념이다. 수학적으로는 해당 점에서의 기울기(미분값)가 0인 지점이다.
최대값/최소값 (Global Maximum/Minimum): 산맥 전체를 통틀어서 가장 높거나 낮은 지점이다. 에베레스트산 같은 개념이다.
주의점: 미분을 통해 기울기가 0인 지점을 찾았을 때, 그곳이 '동네 봉우리(Local)'인지 '세계 최고봉(Global)'인지 바로 알 수는 없다. 그래서 전체적인 함수의 모양을 파악하는 것이 중요하다.

2. 그라디언트 (Gradient, del f)

변수가 하나일 때는 미분(Derivative)이라고 부르지만, 변수가 여러 개(x, y, z 등)일 때는 이를 확장한 '그라디언트'라는 개념을 사용한다.

정의: 각 변수로 편미분(특정 변수만 주인공으로 보고 나머지는 상수로 취급하여 미분하는 것)한 값들을 한데 모아놓은 벡터다.
- 표현: Gradient f = [df/dx, df/dy]
성질과 목적: 그라디언트는 "함수 값이 가장 가파르게 증가하는 방향"을 가리킨다.
- 산 위로 빨리 올라가고 싶다면 그라디언트 방향으로 가면 되고, 빨리 내려오고 싶다면 그라디언트의 반대 방향(-Gradient f)으로 가면 된다. 이를 이용한 알고리즘이 그 유명한 경사하강법(Gradient Descent)이다.
최적점의 조건: 가장 높은 곳이나 낮은 곳에 도달하면 더 이상 올라갈 곳도 내려갈 곳도 없으므로, 그라디언트 값은 0 (영벡터)이 된다.

3. 헤시안 행렬 (Hessian Matrix, H)

그라디언트가 "어디가 가파른가?"를 알려준다면, 헤시안은 "지형이 어떻게 굽어 있는가(곡률)?"를 알려주는 역할을 한다.

정의: 함수를 두 번 미분(2차 미분)하여 만든 행렬이다. 모든 변수 조합에 대해 두 번씩 미분한 값들을 표처럼 정리한 것이다.
- 2변수 함수의 예시:
  H =
- [ f_xx, f_xy ]
  [ f_yx, f_yy ]
  (f_xx는 x로 두 번 미분, f_xy는 x로 한 번 미분 후 y로 다시 미분한 값)
역할 (2차 도함수 판정법):
그라디언트가 0인 지점을 찾았을 때, 이곳이 봉우리(극대)인지 골짜기(극소)인지 판별해 준다.
- 헤시안이 양수(+) 느낌(Positive Definite)이면: 아래로 볼록한 골짜기(극소)이다.
- 헤시안이 음수(-) 느낌(Negative Definite)이면: 위로 볼록한 봉우리(극대)이다.
- 말 안장 모양(Saddle Point): 어떤 방향으론 골짜기인데 어떤 방향으론 봉우리인 지점도 존재한다. 이때 헤시안은 이 지점이 "가짜 최적점"임을 알려준다.

볼록 함수 (Convex Function): 아래로 볼록한 모양이다. 즉, 그릇이나 골짜기 형태다. 밥그릇을 바닥에 놓은 모양이라고 생각하면 된다.
- 볼록 함수(Convex)의 경우:
  - 어디서 시작하든 '경사하강법'을 써서 내려가다 보면 결국 바닥에 도달한다.
  - 이때 찾은 극소점(Local Minimum)이 무조건 전체에서의 최솟값(Global Minimum)이 된다.
오목 함수 (Concave Function): 위로 볼록한 모양이다. 즉, 무덤이나 산봉우리, 돔(Dome) 형태다. 밥그릇을 거꾸로 뒤집어 놓은 모양이다.
- 오목 함수(Concave)의 경우:
  - 위로 계속 올라가다 보면 결국 꼭대기에 도달한다.
  - 이때 찾은 극대점(Local Maximum)이 무조건 전체에서의 최대값(Global Maximum)이 된다.

실제 사례
- 머신러닝(딥러닝): 우리가 인공지능을 학습시킬 때 쓰는 '손실 함수(Loss Function)'가 볼록(Convex)하다면, 인공지능은 아주 쉽게 최적의 정답을 찾을 수 있다. 만약 볼록하지 않고 울퉁불퉁하다면, Local Minimum에 빠져서 정답을 못 찾을 수도 있다.
- 경제학(효용 함수): 보통 인간의 만족도를 나타내는 효용 함수는 오목(Concave)하다고 가정한다. 돈이 많아질수록 추가로 얻는 기쁨은 점점 줄어들기 때문에(한계효용 체감), 그래프가 산 모양으로 굽어지기 때문이다.
최적화 3단계 로직 (볼록/오목 포함)
- 그라디언트(Gradient) 구하기: 어디로 가야 할지 방향을 정한다.
  - 그라디언트 = 0 인 지점 찾기: 평평한 후보지를 찾는다.
  - 헤시안(Hessian)으로 성격 파악하기:
    - 헤시안이 양수(+)면? -> 볼록(Convex)한 지형의 최솟값을 찾은 것이다.
    - 헤시안이 음수(-)면? -> 오목(Concave)한 지형의 최대값을 찾은 것이다.
    - 헤시안이 섞여 있으면? -> 더 찾아봐야 한다.

4. 최적화의 3단계 로직

그라디언트(Gradient f)를 구한다: "어디가 가파른가? 어디로 가야 하는가?" (방향 파악)
Gradient f = 0 인 지점을 찾는다: "후보지를 찾았다. 여기는 일단 평평하다." (후보지 선정)
헤시안(H)을 확인한다: "여기가 골짜기인가, 봉우리인가, 아니면 말 안장인가?" (상태 확정)

이걸 왜 배우는가?

행렬(선형대수): 수만 개의 데이터를 하나의 기호(A)로 묶어 처리하기 위해서다.
미분(최적화): 손실은 최소화하고 수익은 최대화하는 최적의 파라미터를 찾기 위해서다.
적분: 변화율을 모아 전체 양(확률, 누적값)을 계산하기 위해서다.

데이터, Python이 소고기, 돼지고기 단백질이라면

기초수학, 기초통계는 야채다..

앞으로 경영 통계, 머신러닝, 재무 모델링 수업의 수식들을 멍 때리고 보지 않기 위한 자산이 될 것이다.

[DFMBA] 기초수학 Wrap-Up